 Altough they are not strictly part of mathematics since they are used often
in informatics we decided to show how to represent them in Latex.
The package "forest" is needed.
Altough they are not strictly part of mathematics since they are used often
in informatics we decided to show how to represent them in Latex.
The package "forest" is needed.A tree diagram consist of an element from wich 1 or more other elements are derived, these elements could also divide in 1 or many others until an element from wich nothing derives is reached. The following example represents a general tree diagram.
 To make a tree we need to use:
To make a tree we need to use:
\begin{forest}
...
\end{forest}
The element following the root are considered from left to right.
Every element of a tree can be considered as a root for a subtree, for example a0 in the last image can be considered as a root to the following tree:
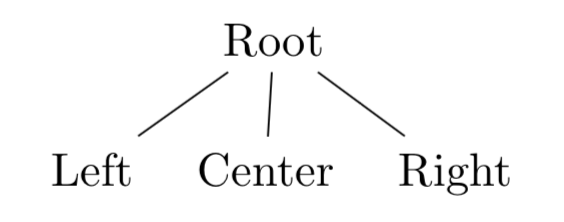
 This said, let's make a tree step by step.
This said, let's make a tree step by step.The root must be inside square brackets that must also contain all elements that derive from it. To start let's make a tree with a root and three following elements.
\begin{forest}
[Root
[Left]
[Center]
[Right]
]
\end{forest}
 To make a tree in wich some elements branches it is enough to replace
those elements with the desired subtree. This said let's modify our last
tree so that the center element has two subelements, center-left and
center-right.
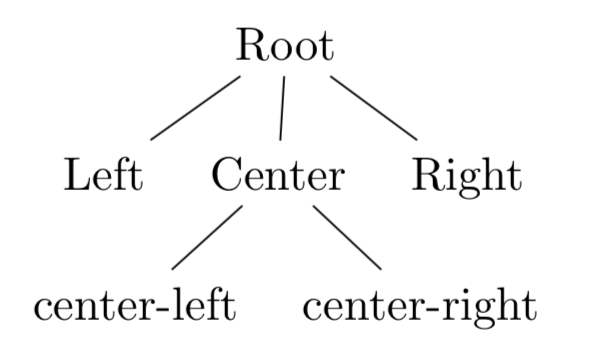
To make a tree in wich some elements branches it is enough to replace
those elements with the desired subtree. This said let's modify our last
tree so that the center element has two subelements, center-left and
center-right.
\begin{forest}
[Root
[Left]
[Center
[center-left]
[center-right]
]
[Right]
]
\end{forest}
 It should now be quite clear how to make any desired tree. This said,
there are still a couple of options that may come in handy.
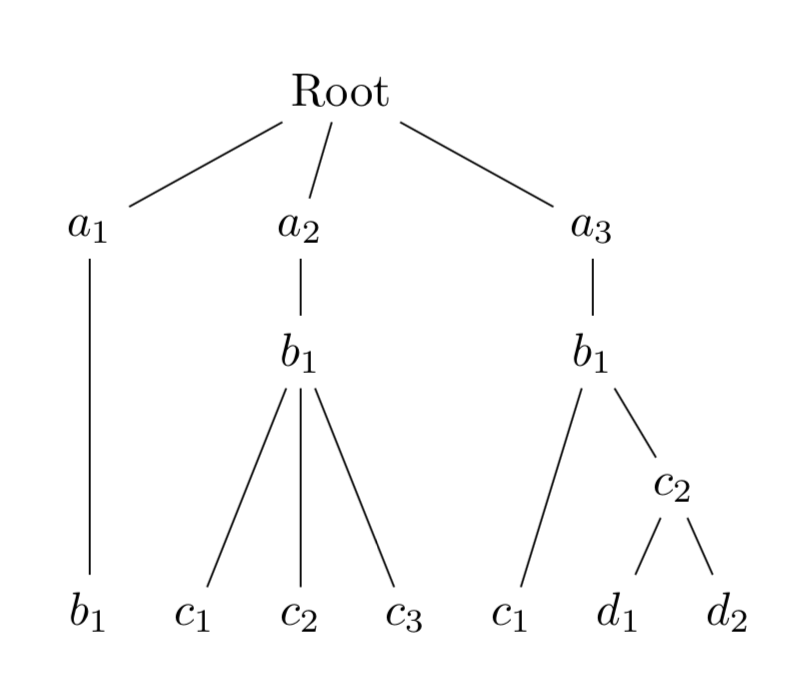
It should now be quite clear how to make any desired tree. This said,
there are still a couple of options that may come in handy.The first option will align all leaves:
\begin{forest}
for tree={
if n children=0{
font=\itshape,
tier=terminal,
}{},
}
[Root
[$a_1$
[$b_1$]]
[$a_2$
[$b_1$
[$c_1$]
[$c_2$]
[$c_3$]]]
[$a_3$
[$b_1$
[$c_1$]
[$c_2$
[$d_1$]
[$d_2$]]]]]
\end{forest}
 We might want to put each element inside a figure, let's say a circle,
and let's change the color of the nodes as well.
This is possible with following code:
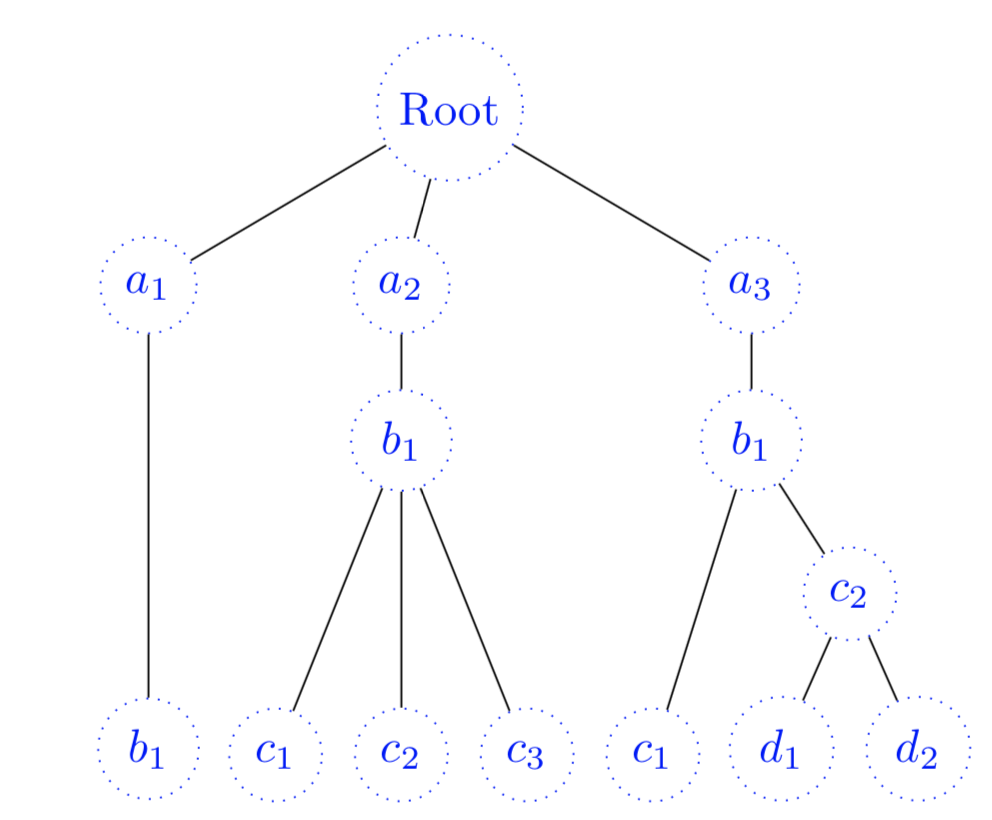
We might want to put each element inside a figure, let's say a circle,
and let's change the color of the nodes as well.
This is possible with following code:
\begin{forest}
for tree={draw,circle,dotted,blue
if n children=0{
font=\itshape,
tier=terminal,
}{},
}
[Root
[$a_1$
[$b_1$]]
[$a_2$
[$b_1$
[$c_1$]
[$c_2$]
[$c_3$]]]
[$a_3$
[$b_1$
[$c_1$]
[$c_2$
[$d_1$]
[$d_2$]]]]]
\end{forest}
 One last option that might be interesting let us draw around a subtree,
this might be useful to highlight some part of our tree. To achive this
it is enough to add the following code after an element of the tree, it
will highlight that element and all elements that derive from it.
One last option that might be interesting let us draw around a subtree,
this might be useful to highlight some part of our tree. To achive this
it is enough to add the following code after an element of the tree, it
will highlight that element and all elements that derive from it.
[Node,tikz={\node [draw,red,inner sep=0,fit to=tree]{};}...
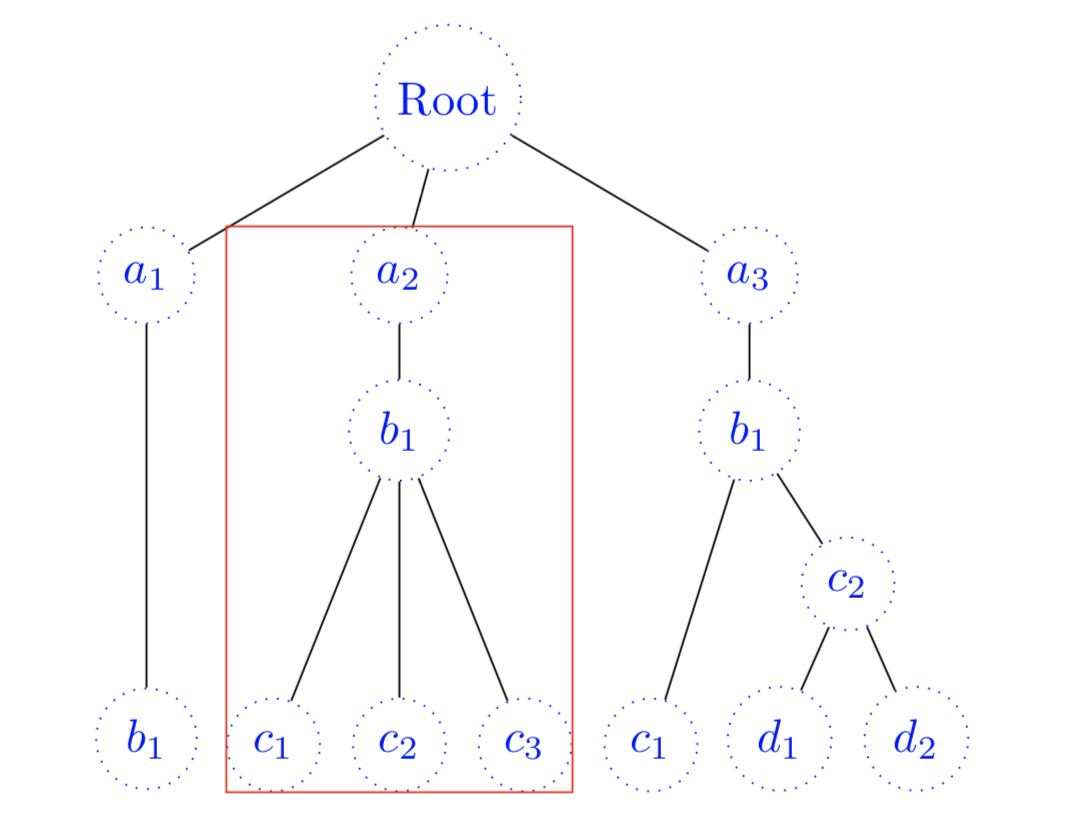 This informations should suffice to make a decent tree diagram, but of
corse this is only the tip of the iceberg and many more options are avaible
to make even better diagrams.
This informations should suffice to make a decent tree diagram, but of
corse this is only the tip of the iceberg and many more options are avaible
to make even better diagrams.
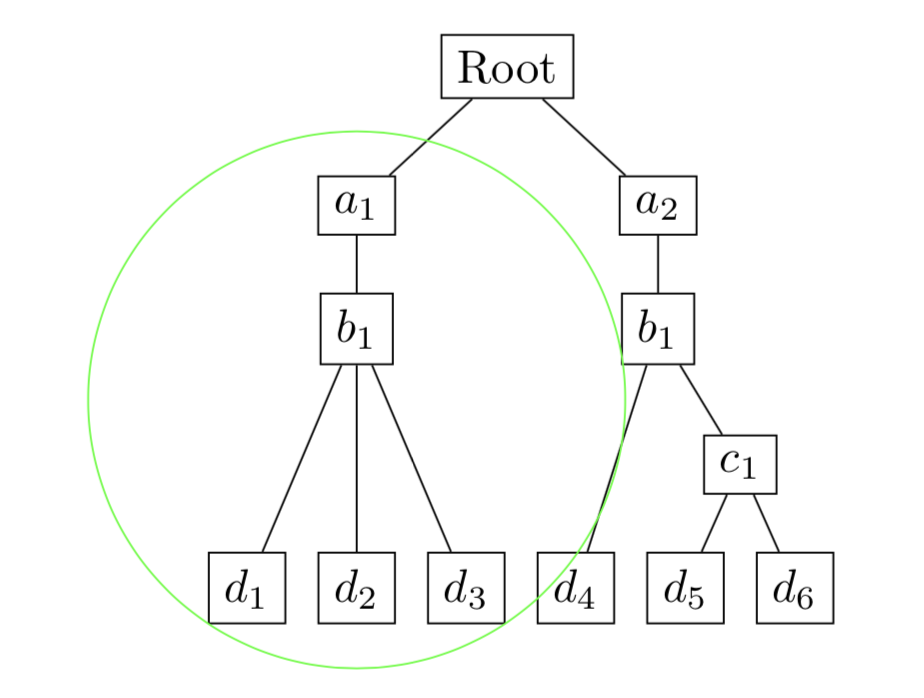
To check that all these new concepts have been understood i would
like to invite the reader to try and replicate the following diagram using
Latex.
for tree={draw,
if n children=0{
font=\itshape,
tier=terminal,}{},}
[Root
[$a_1$ ,tikz={\node [draw,circle,green,inner sep=0,fit to=tree]{};}
[$b_1$
[$d_1$]
[$d_2$]
[$d_3$]]]
[$a_2$
[$b_1$
[$d_4$]
[$c_1$
[$d_5$]
[$d_6$]]]]]
