Equations - Symbols

Symbols

On this page you will find a glossary of the main mathematical symbols, cataloged among the main branches of mathematics in which they are most widely used. Indeed you will use some of these symbols in order to write in the math-language.
Below you will find a list of the illustrated symbol categories.

Greek and Hebrew Letters

These letters are often used in mathematics for variables, constants and unknowns.

Name	Symbol	Command
alpha	α	\alpha
beta	β	\beta
chi	χ	\chi
delta	δ	\delta
epsilon	ε	\epsilon
eta	η	\eta
gamma	γ	\gamma
iota	ι	\iota
kappa	κ	\kappa
lambda	λ	\lambda
mu	μ	\mu
nu	ν	\nu
o	o	o
omega	ω	\omega
phi	φ	\phi
pi	π	\pi
psi	ψ	\psi
rho	ρ	\rho
sigma	σ	\sigma
tau	τ	\tau
theta	θ	\theta
upsilon	υ	\upsilon
xi	ξ	\xi
zeta	ζ	\zeta
digamma	ϝ	\digamma
varepsilon	ϵ	\varepsilon
varkappa	ϰ	\varkappa
varphi	ϕ	\varphi
varpi	ϖ	\varpi
varrho	ϱ	\varrho
varsigma	ς	\varsigma
vartheta	ϑ	\vartheta
Delta	Δ	\Delta
Gamma	Γ	\Gamma
Lambda	Λ	\Lambda
Omega	Ω	\Omega
Phi	Φ	\Phi
Pi	Π	\Pi
Psi	Ψ	\Psi
Sigma	Σ	\Sigma
Theta	Θ	\Theta
Upsilon	Υ	\Upsilon
Xi	Ξ	\Xi
aleph	ℵ	\aleph
beth	ℶ	\beth
daleth	ℸ	\daleth
gimel	ℷ	\gimel

CODE

$$\iota \alpha \tau \varepsilon \chi$$

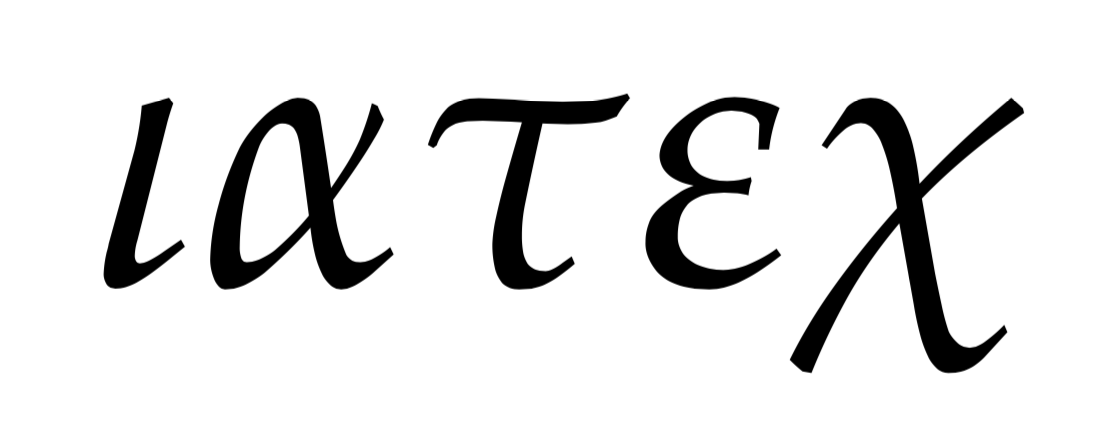
Number Sets

Mathematical sets are essential when we have to define to which of these a number belongs, in order to exploit certain properties or carry out certain operations.

Name	Symbol	Command
Prime	P	\mathbb{P}
Whole	W	\mathbb{W}
Natural	N	\mathbb{N}
Integers	Z	\mathbb{Z}
Irrational	I	\mathbb{I}
Rational	Q	\mathbb{Q}
Real	R	\mathbb{R}
Complex	C	\mathbb{C}

CODE

$$\mathbb{Z}\in\mathbb{R}\notin\mathbb{N}$$

Brackets

When we are faced with numerical expressions of certain dimensions it is essential to maintain an order, so it is important to define different types of brackets, each of which indicates a certain priority of calculation.

Name	Symbol	Command
Round Brackets	( ... )	\left( ... \right)
Square Brackets	[ ... ]	\left[ ... \right]
Braces	{ ... }	\left{ ... \right}
Angle Brackets	⟨ ... ⟩	\langle ... \rangle

CODE

$$\left \{ 2 \left [ 6 \left ( 5+1 \right )\right ] \right \} = 72$$

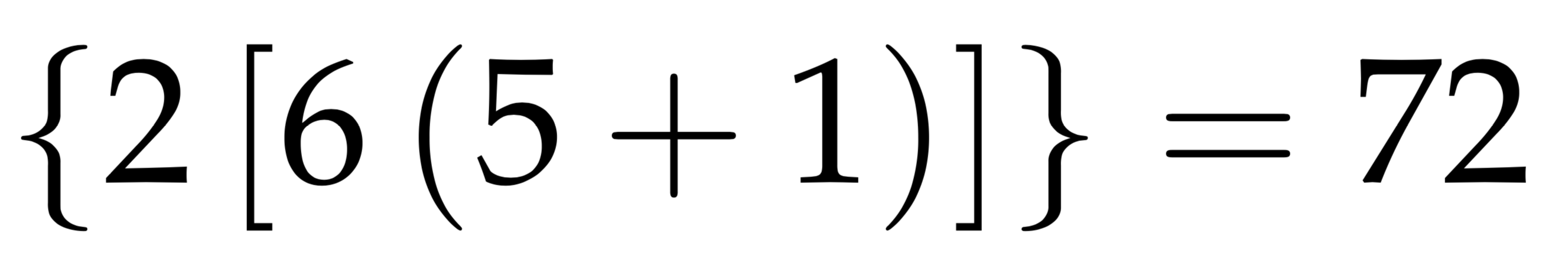
Principal Relation Symbols

These symbols allow us to show characteristics of certain elements.

Name	Symbol	Command
Equivalent	≡	\equiv
Congruent	≅	\cong
Equal	=	\=
Not equal	≠	\neq
Less or equal	≤	\leq
Greater or equal	≥	\geq
Such that	\|	\mid
Subset	⊂	\subset
Superset	⊃	\supset
Element of	∈	\in
Not element of	∉	\notin

CODE

$$0 \leq 10 > 5 = 5 \neq 2.5 \notin \mathbb{R}$$

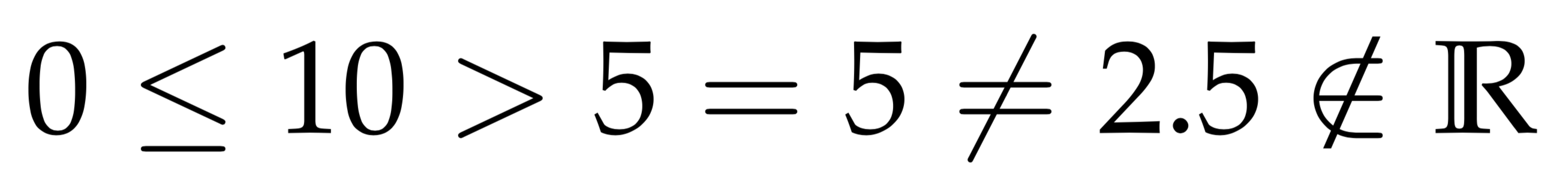
Principal Arrow Symbols

In mathematics the arrows have different uses, one of these is for example that of showing the equivalence between two equations.

Name	Symbol	Command
Left arrow	←	\leftarrow
Right arrow	→	\rightarrow
Left-right arrow	↔	\leftrightarrow
Left double arrow	⇐	\Leftarrow
Right double arrow	⇒	\Rightarrow
Left-right big arrow	⇔	\geq
Left long arrow	⟵	\longleftarrow
Right long arrow	⟶	\longrightarrow
Left-right long arrow	⟷	\longleftrightarrow
Left long double arrow	⟸	\Longleftarrow
Right long double arrow	⟹	\Longrightarrow
Left-right long double arrow	⟺	\Longleftrightarrow
Right arrow from bar	↦	\mapsto
Right long arrow from bar	⟼	\longmapsto

CODE

$$5 + \alpha = 3 \Leftrightarrow \alpha = 3 - 5 \Leftrightarrow \alpha = -2\\

            \rightarrow \alpha = -5$$

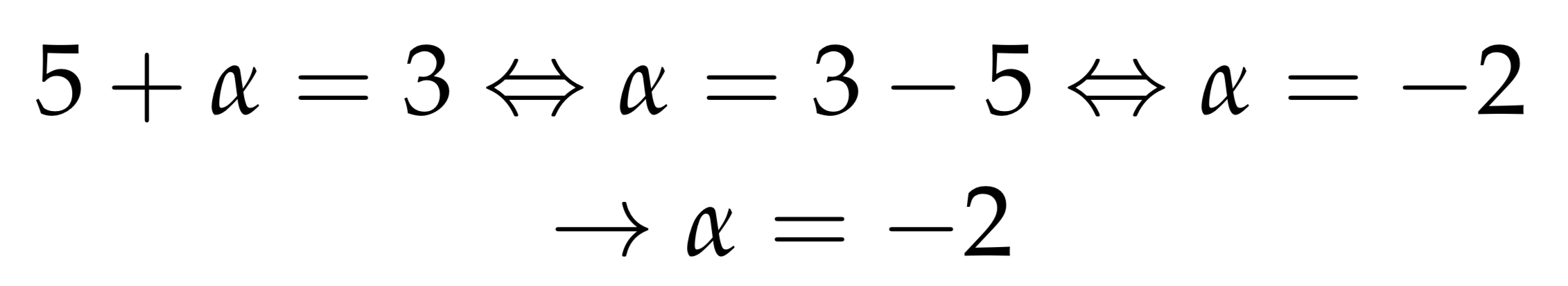
Miscellaneous Symbols

These are some symbols not belonging to the other categories, very often used in mathematics.

Name	Symbol	Command
Infinity	∞	\infty
Plus-minus	±	\pm
Percentage	%	\%
Ellipsis	. . .	\cdots
Vertical ellipsis	⋮	\vdots
Oblique ellipsis	-	\ddots

CODE

$$\infty\pm10\%\infty=\infty$$

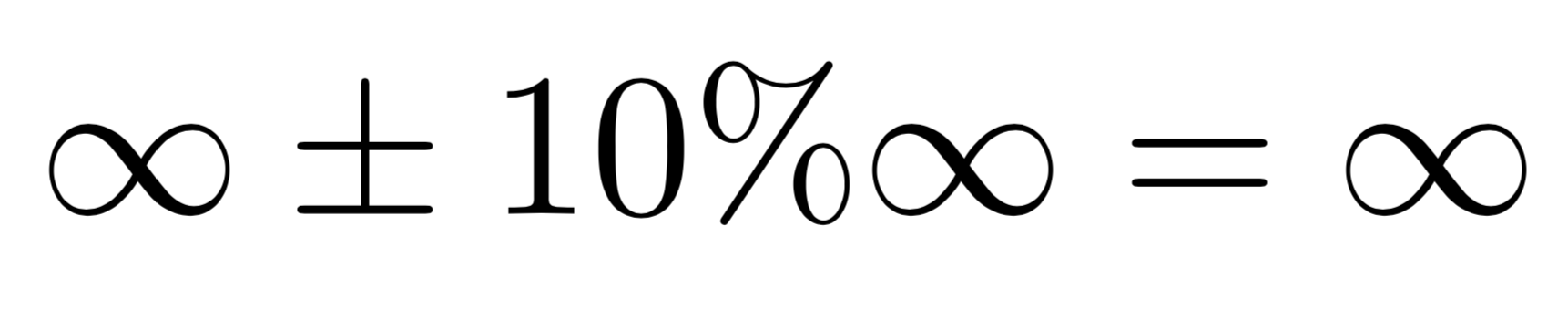
Exercices

1) Write down the code necessary to describe a number set in N which contains α, χ and δ. The set doesn't belong to R. In a second line specify that α > δ and α ≤ χ.

$$\left \{ \alpha;\chi;\delta \right \} \in \mathbb{N} \notin \mathbb{R}$$

            $$\alpha>\delta\\, \alpha\leq\chi$$

2) Use one of the two given right arrow from bar in order to built a function which, from two output γ and ω, returns a prime number P.

$$\left ( \gamma, \omega \right ) \mapsto f\left ( \gamma, \omega \right ) \in \mathbb{P}$$